> [!META]- Inline Metadata
> [tags:: #career #concepts/programming/algorithms/binary-search ]
> [project group:: Neetcode 150]
> [difficulty:: medium]
> [status:: to begin]
> [link:: https://leetcode.com/problems/search-a-2d-matrix/]
> [up:: [[Leetcode MOC]]]
## Problem
You are given an `m x n` integer matrix `matrix` with the following two properties:
- Each row is sorted in non-decreasing order.
- The first integer of each row is greater than the last integer of the previous row.
Given an integer `target`, return `true` _if_ `target` _is in_ `matrix` _or_ `false` _otherwise_.
You must write a solution in `O(log(m * n))` time complexity.
**Example 1:**

**Input:** `matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3`
**Output:** `true`
**Example 2:**
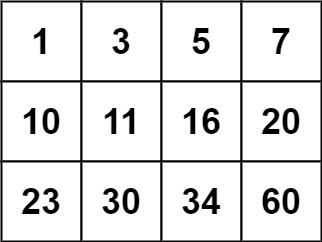
**Input:** `matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13`
**Output:** `false`
**Constraints:**
- `m == matrix.length`
- `n == matrix[i].length`
- `1 <= m, n <= 100`
- `-10e4 <= matrix[i][j], target <= 10e4`
## Solution
### Mine
#### Python
```python
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
row_1_idx, row_2_idx = 0, len(matrix) - 1
while row_1_idx <= row_2_idx:
if row_1_idx == row_2_idx:
return self._search_row(matrix[row_1_idx], target)
mid_row_idx = (row_1_idx + row_2_idx) // 2
if matrix[mid_row_idx][-1] > target and matrix[mid_row_idx][0] < target:
return self._search_row(matrix[mid_row_idx], target)
elif matrix[mid_row_idx][-1] > target:
row_2_idx = mid_row_idx
elif matrix[mid_row_idx][-1] < target:
row_1_idx = mid_row_idx + 1
elif matrix[mid_row_idx][-1] == target:
return True
return False
def _search_row(self, row: List[int], target: int) -> bool:
left, right = 0, len(row) - 1
while left <= right:
midpoint = (left + right) // 2
if row[midpoint] > target:
right = midpoint - 1
elif row[midpoint] < target:
left = midpoint + 1
else:
return True
return False
```
#### Rust
### LC's
## Things I Learned
### Neetcode Video
$O (m\space log \space n)$ would be binary search on each row, but we can do better.
Running binary search (as I did) on all the rows is $O (log\space m)$, then by doing the row binary search makes the total $O(log \space m) + O(log \space n) \rightarrow O(log(m + n))$.
```python
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
ROWS, COLS = len(matrix), len(matrix[0])
top, bot = o, ROWS - 1
while top <= bot:
row = (top + bot) // 2
if target > matrix[row][-1]:
top = row + 1
elif target < matrix[row][0]:
bot = row - 1
else:
break
if not (top <= bot):
return False
# Do binary search on target row
row = (top + bot) // 2
l, r = 0, COLS - 1
while l <= r:
m = (l + r) // 2
if target > matrix[row][m]:
l = m + 1
elif target < matrix[row][m]:
r = m - 1
else:
return True
return False
```
## Scratchpad
Initial idea would be to merge all lists, then binary search them. Extra space would be $O(m)$, time should be $O(m\space log\space n)$? $m$ to merge, $log \space n$ for binary search?
Can't do this because flattening is actually $O(mn)$.
The other thing I want to try is to do a binary search on the rows: take middle row, check first or last item, then middle of that, continue? The idea is to reduce the matrix to a single candidate row, then binary search that row.